Sugar & Salt Corner
No. 45
2011年5月29日
佐藤 敏雄
π(パイ)のお話
― 神はπに何を隠したのか ―
 マンスリーレターNo.7で紹介された素数に続き、変な数、円周率πのお話です。
マンスリーレターNo.7で紹介された素数に続き、変な数、円周率πのお話です。先頃NHKで釈由美子がオーナーの「しびれるレストラン」で放映されたのでご覧になった方もあると思いますが、おかしな数列をもう一度眺め直して頂くのも一興かと。
因みにπという字は、「周囲」と言う意味のギリシャ語περιφερεια(ペリフェレイア)の頭文字です。英語の peripheralはこのギリシャ語から来ており、パソコンの周辺機器がペリフェラルと呼ばれるのもここから。
πは円周の長さと直径の比で3.14が広く使われていますが、実は無限に続く数列であることはご存知の通りです。いかなる代数方程式の根にもならない超越数と呼ばれます。このπについては、4000年もの昔から多くの説明がなされてきました。

初めて理論的に取り組んだのはギリシャの哲学者アルキメデス(287BC〜212BC)。彼は「円周の長さは、その円に内接する多角形の辺の全長より長く、外接する多角形の辺の全長より短い」ことに着目して96角形まで計算しました。
その結論は、「πの値は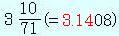
より大きく、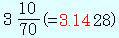 より小さい」。
より小さい」。
円周率:3.14はここに始まります。爾来、今世紀に至るまで、古今東西、多くの天才がπの値に挑戦してきました。
ドイツのルドルフ(1540〜1610) は「461京1686兆184億2738万7904角形」について、ペンと紙だけで計算し、小数点以下35桁まで算出しました。彼は、計算開始から40年後に亡くなりましたが、その遺言通り、彼の墓碑銘にはこの35桁が記されているそうです。
17世紀には、次のようなグレゴリー・ライプニッツの公式が発見されました。
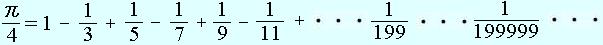
この式で、100項、つまり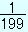 まで計算すると分母・分子共に88桁の分数となります
まで計算すると分母・分子共に88桁の分数となります が、通分して得られる膨大な分数の計算で得られる答えは、3.1315・・・。合計10万個の奇数を使って計算しても、3.142582653・・・
と小数点以下4桁しか正しい値になりません。円とは全く関係の無い、この奇妙な奇数とπの関係。ライプニッツ(1646〜1716)は、「神は奇数を喜ばれる」と言ったとか。
が、通分して得られる膨大な分数の計算で得られる答えは、3.1315・・・。合計10万個の奇数を使って計算しても、3.142582653・・・
と小数点以下4桁しか正しい値になりません。円とは全く関係の無い、この奇妙な奇数とπの関係。ライプニッツ(1646〜1716)は、「神は奇数を喜ばれる」と言ったとか。
次は「ビュフォン伯爵(1707〜1788)の針」。間隔dで平行な直線を何本か引きます。その上から、間隔dの半分の長さの針を落としたとき、その針が平行な線に触れる確率は1/πだそうです。これも円とは関係ないですね。
わが国でも江戸時代の算学者 建部賢弘(1664〜1739)は、多角形の辺の数の増加に対する答の出方の変化に着目するという鋭い洞察に基づき、1024角形について10日間、不眠不休で算盤をはじき、41桁まで計算しています。当時としては世界最高の値です。
18世紀半ばには、かの有名な数学者オイラー(1707〜1783)(下の写真)が、
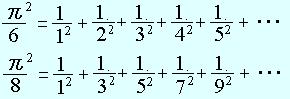
など、200に及ぶπ計算の公式を発見しています。
中でも最も有名なのは、オイラーの等式:
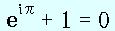
(e は自然対数の底、i は虚数単位)
です。後に物理学や電子工学に導入され、近代文明の基礎を作りました。この式には、我々通信技術者は大いに悩まされたものです。
π計算の歴史についてはネットにゴマンと出ていますので、この辺にしておきましょう。
1948年、米国で開発されたコンピュータENIACを使い、2047桁まで計算されましたが、真空管を使ったこの機械は故障ばかりしていました。東大では、9年前にスーパーコンピユータにより、1兆2000桁まで計算しましたが、やはり膨大な数の部品の不具合が問題だそうです。
そんな計算をして何の役に立つのかと言いたくなりますが、今では逆に2つの違うπの計算式を開発中のコンピュータに計算させ、両者の答えが一致するかどうかでその信頼性をチェックするのだそうです。メーカーでは想定外だった設計ミスを発見し、スーパーコンピュータの発達に寄与しているそうです。
ところで、昨年8月、長野県飯田市にお住まいの近藤茂さんという会社員の方が、自作のパソコンでπを5兆桁まで計算し、ギネスに認定されるという、とんでもない快挙を成し遂げられました。使ったメモリーは24テラバイト。ハードディスクを16台使い、90日かけて算出したそうです。因みに5兆桁目の数字は「2」。5兆の数列に現れる数字の出現頻度はどれもほぼ同じで、それぞれ5000億回ほど。最も多く現れるのは「8」だとか。
その数列の中には、1の連続とか、0から9まで連続する数字とか、例えば釈由美子の誕生日?19780612なども見つかるそうです。近藤さん、定年後は10兆桁計算を目指しておられるそうですから驚きです。
πには我々の生活に密接な関係を持つものが多々あります。例えば、所定の号数(サイズ)に合わせた指輪を作るのに必要な地金の長さを決めるためには3.14が使われるとか、陸上競技のトラックの半円周部分の計算には3.1416を使うとルールブックに出ているとか。砲丸投げの砲丸を正確に作るためには9桁(3.141592653)が使われているそうです。
その結論は、「πの値は
より大きく、
円周率:3.14はここに始まります。爾来、今世紀に至るまで、古今東西、多くの天才がπの値に挑戦してきました。
ドイツのルドルフ(1540〜1610) は「461京1686兆184億2738万7904角形」について、ペンと紙だけで計算し、小数点以下35桁まで算出しました。彼は、計算開始から40年後に亡くなりましたが、その遺言通り、彼の墓碑銘にはこの35桁が記されているそうです。
17世紀には、次のようなグレゴリー・ライプニッツの公式が発見されました。
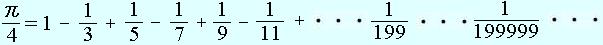
この式で、100項、つまり
 が、通分して得られる膨大な分数の計算で得られる答えは、3.1315・・・。合計10万個の奇数を使って計算しても、3.142582653・・・
と小数点以下4桁しか正しい値になりません。円とは全く関係の無い、この奇妙な奇数とπの関係。ライプニッツ(1646〜1716)は、「神は奇数を喜ばれる」と言ったとか。
が、通分して得られる膨大な分数の計算で得られる答えは、3.1315・・・。合計10万個の奇数を使って計算しても、3.142582653・・・
と小数点以下4桁しか正しい値になりません。円とは全く関係の無い、この奇妙な奇数とπの関係。ライプニッツ(1646〜1716)は、「神は奇数を喜ばれる」と言ったとか。次は「ビュフォン伯爵(1707〜1788)の針」。間隔dで平行な直線を何本か引きます。その上から、間隔dの半分の長さの針を落としたとき、その針が平行な線に触れる確率は1/πだそうです。これも円とは関係ないですね。
わが国でも江戸時代の算学者 建部賢弘(1664〜1739)は、多角形の辺の数の増加に対する答の出方の変化に着目するという鋭い洞察に基づき、1024角形について10日間、不眠不休で算盤をはじき、41桁まで計算しています。当時としては世界最高の値です。
18世紀半ばには、かの有名な数学者オイラー(1707〜1783)(下の写真)が、

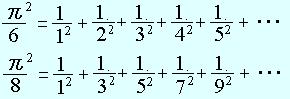
など、200に及ぶπ計算の公式を発見しています。
中でも最も有名なのは、オイラーの等式:
(e は自然対数の底、i は虚数単位)
です。後に物理学や電子工学に導入され、近代文明の基礎を作りました。この式には、我々通信技術者は大いに悩まされたものです。
π計算の歴史についてはネットにゴマンと出ていますので、この辺にしておきましょう。
1948年、米国で開発されたコンピュータENIACを使い、2047桁まで計算されましたが、真空管を使ったこの機械は故障ばかりしていました。東大では、9年前にスーパーコンピユータにより、1兆2000桁まで計算しましたが、やはり膨大な数の部品の不具合が問題だそうです。
そんな計算をして何の役に立つのかと言いたくなりますが、今では逆に2つの違うπの計算式を開発中のコンピュータに計算させ、両者の答えが一致するかどうかでその信頼性をチェックするのだそうです。メーカーでは想定外だった設計ミスを発見し、スーパーコンピュータの発達に寄与しているそうです。
ところで、昨年8月、長野県飯田市にお住まいの近藤茂さんという会社員の方が、自作のパソコンでπを5兆桁まで計算し、ギネスに認定されるという、とんでもない快挙を成し遂げられました。使ったメモリーは24テラバイト。ハードディスクを16台使い、90日かけて算出したそうです。因みに5兆桁目の数字は「2」。5兆の数列に現れる数字の出現頻度はどれもほぼ同じで、それぞれ5000億回ほど。最も多く現れるのは「8」だとか。
その数列の中には、1の連続とか、0から9まで連続する数字とか、例えば釈由美子の誕生日?19780612なども見つかるそうです。近藤さん、定年後は10兆桁計算を目指しておられるそうですから驚きです。

πには我々の生活に密接な関係を持つものが多々あります。例えば、所定の号数(サイズ)に合わせた指輪を作るのに必要な地金の長さを決めるためには3.14が使われるとか、陸上競技のトラックの半円周部分の計算には3.1416を使うとルールブックに出ているとか。砲丸投げの砲丸を正確に作るためには9桁(3.141592653)が使われているそうです。
最後に、あの「はやぶさ」が大気圏に再突入する時に必要な減速ベクトルの計算には15桁のπが使われたと、宇宙研の的場先生が話しておられました。3.14を使ったのでは、地球から15万キロ離れた空間を通過してしまい、地球に帰還できなかったそうです。
やれやれ、哲人の言葉で締めくくることとしましょう。
「πは神の最高傑作である」
やれやれ、哲人の言葉で締めくくることとしましょう。
「πは神の最高傑作である」
以上